I do a lot of walking in the countryside, and it was on one such walk earlier this year, that I stopped to take in the vista shown below. It was late autumn/fall, and due to a combination of a hot summer, and recent fine weather, the golden foliage had not fallen as yet. As I allowed myself to become absorbed in the structure around me, I was thinking about how nature creates such rich and beautiful scenes. It is, of course, cliché to say that a photograph cannot capture the true beauty. It seems that no matter where you point and whatever you crop you lose some of the essential form. Either at the large scale, or texture, at the small scale, some part that is necessary to cognise the true beauty is lost. Though I am sure a master photographer could do a better job, the resulting photograph would still be a mere pale representation of reality.

Figure 1: Natural Woodland
I don’t believe it would be possible for a gardener, or indeed any human, to create this kind of landscape. Even though the building blocks of a garden, the plants, rocks, and earth, are the same there is something intrinsically different. Again, this is not to say expert gardeners cannot have the vision, creativity, and skill to create a beautiful garden. The result, though, is different, and of course, deliberately so. However, the thing is that a newly created garden resembles a building site. It is only through the work of nature that the edges are softened, and the beauty can emerge.
The intrinsic mechanisms that determine the behaviour of organisms cause them to live and grow. They do this in such a way to optimise their survival, and maximally utilise the environment in which they live. It is the emergent structure from the life force that creates what we see.
Beauty it seems is closely related to life. Maybe it is that the things we find beautiful are conducive to life in the sense that things that are good for us, things that we need, and things that we like, they have value to our life. They make life easier or even possible. Therefore we see them as beautiful. That’s our way of measuring it even though we can’t objectively say what it is.
There is something similar going in architecture. I am not sure architecture is the right word for what I mean. What I’m talking about is the structure of our living spaces from rooms, to buildings, to towns and cities. When these evolve naturally, through the people living and adapting them incrementally, through the requirements of their life, and the forces of what’s around them, something beautiful emerges. Though this happens through the deliberate actions of humans, when it happens without an overall plan, when it happens through small incremental decisions, the overall evolution is organic. Good decisions are made which ease and aid the lives of people living there.
I’ve always been intrigued by why it is so much more desirable to be around ancient architecture than the modern. You see this when people go travelling. They hang out in the old town. People enjoy being there - it makes them feel good. The interest, the feeling — people just want to be there. My personal experience is that it brings out a natural curiosity. Around each corner lies a new vista and a multitude of options for exploration.
I’m not happy with not being able to not objectively say what this feeling is. Ideally, I want a theory behind it and an algorithm. Back in the 1990s, I discovered the work of Christoper Alexander through a link to the nascent work in design patterns in software. I read every one of his books and was particularly consumed by the work “A Pattern Language.” This codified a set of interrelated patterns, which always seemed to appear when “the timeless way of building” was used. This timeless way, Alexander said, has been largely ignored in the last century, but before this, and across the world, it was the default way. This pattern language has a fractal-like structure from regional scale all the way down to the minutest of details within the layout or decoration of a room. At the time I created a hyperlinked summary of the book which aided my understanding. The patterns describe the natural tension of conflicting forces, and how the pattern helps to optimise the outcome in these situations. This is fascinating stuff even if you’re not an architect.
It should be said that Alexanders work is controversial. Contemporary architects see his works as conservative in aspiration at best and at worst fundamentally sentimental and Luddite. I don’t take that view. There is a large amount of politics in most disciplines, and Alexander’s approach challenged the modern view of architecture and town planning. He said there was little room for arbitrary (fashion) based designs or being different to make a statement.
Since Alexander published his works on architecture, he has focused on broadening the scope of this approach. Generalising and unifying the patterns, he has evolved it into a philosophy that encompasses everything. This could easily be seen as the indulgences in the late stages of a successful career. In many ways, his massive 4 volume, 2000 page work, “The Nature of Order” is just that. However, I believe he has succeeded in distilling the essence of what life creates and what beauty is, and that is no small feat.
Alexander puts down a foundation of 15 abstract geometric properties of patterns, which together, aim to characterise life, and things that exhibit life. Let’s quickly step through these patterns now:
- Levels of Scale - Patterns of centers repeat at many levels of scale. Ratios between the scales are not explicitly defined but must not be too large or too small.
- Strong Centers - Centers are a field-like effect that acts as the focus to parts of the structure nearby.
- Boundaries - At the edges of influence of a center, clear but thick boundaries are present.
- Alternating Repetition - Patterns of repetition are usually an alternating pattern of two differing centers.
- Positive Space - Positive space is space outside of centers that form a self-contained structure in its own right.
- Good Shape - Interesting closed shapes of structure around centres that link minor centers to major centers.
- Local Symmetries - Centers are made stronger by symmetry in the patterns around them.
- Deep Interlock and Ambiguity - The boundary of one center and another is often deeply interlocked, and it is not always clear where one ends, and another starts.
- Contrast - Contrast in form between a center, and those adjacent, help to strengthen them.
- Gradients - Gradients that gradually transition properties of those centers over distance.
- Roughness - Imperfections and irregularities are inevitable; they emerge from the interplay of order and the constraints in which the structure exists.
- Echos - Properties such as angles or proportions repeat again and again.
- The Void - Structure is always balanced by space.
- Simplicity and Inner Calm - Structure is no more complicated than it needs to be to balance the forces and constraints on it - this is Occam’s razor.
- Not Separateness - Everything is connected. The structure of any part of a system is ultimately determined by its relationship to everything else. Every system is connected to adjacent systems.

Figure 2: Alexanders 15 Fundamental Properties of Life
You can see that there is some overlap of behaviour described by these properties. Overall they very strongly suggest a fractal structure. They also suggest a kind of pattern that is neither complete order or complete randomness, but somewhere in between. Pulling a form towards complete order is the property of Simplicity and Inner Calm which dictates the elimination of any unnecessary or arbitrary features. In the opposite direction is Not Separateness: the fact that life ultimately exists in an environment that forces it to interact with what is around it, and Roughness: the fact that fundamental laws of geometry and physics often get in the way of a clean expression of the forces.
From this simple basis, the competing forces interact chaotically through energy minimising iteration. This leads to the expression of the other 12 properties. Chaos theory is a well-studied field of how complexity emerges from many simple premises. This suggests, in theory at least, the completely deterministic outcome for the emergence of life in a given environment. In reality, there is no static outcome; constant competition and emergent behaviour leads to higher levels of fractal behaviour that ultimately is unpredictable and uncomputable.
One surprising aspect to me is how simple mathematical fractals such as the Mandelbrot Set lead to structures resembling life. From the simplest of mathematical functions, through iteration, on the substrate of number theory, these complex forms emerge. In the case of the Mandelbrot Set, the function essentially defines places in the complex-number landscape where infinite iteration is possible.
Something slightly closer to the real forces of life is demonstrated in a Logistic map. This mathematic function, again iterative, models population growth in a limited ecosystem, with both the forces of reproduction and starvation. The function is very simple; each iteration returns the result of the previous iteration multiplied by one minus the result of the previous iteration. At specific scales, this function iterates in a completely chaotic way. (Interestingly it is possible to model this function with a simple electronic circuit call the Chua Circuit as a way of generating pseudo-random output in a non-digital way.)
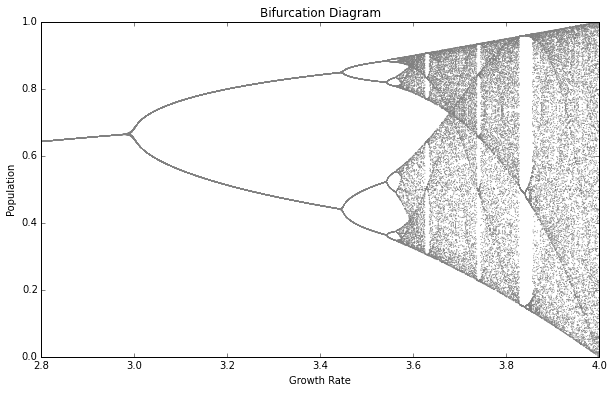
Figure 3: Logistic Map plot
Writing about this stuff is all well and good, but as I mentioned earlier what is important to me is to be able to take these concepts and turn them into hard science. This probably means computer science as that is where my skills lie. There are two concrete branches of exploration here. Firstly how can we take an entity, a building, a photo, a work of art, and determine its merit computationally? If Alexander is correct, it should be possible to determine the relative life of things objectively. The second branch is to find algorithmic ways to generate entities with maximum life.
I suspect from an early investigation that algorithmically generating entities with life will be easier than measuring life. That is unfortunate as I wouldn’t objectively be able to test the results of generation.
As I continue to work on these two branches, I will publish my work here. I have already worked on progressing a two-dimensional measure of life which Alexander presents in an appendix to volume one of The Nature of Order. It’s apparent, though, that his approach is not easily extendible to higher dimensions which is why I spent some time investigating Fourier transforms of interesting fractal forms. I’ve also started exploring generative fractals which model real-life forces. While existing work on L-system fractals generates natural looking forms (through the algorithmic encoding of the rules encoded in the genes of plants), it lacks any approach to iteratively interacting with the environment. Hence it creates forms as islands isolated in their idealised bubbles and frozen in time.
Figure 4: Generative fractal animation
I find this work interesting in and of itself. However, there is a further motivation: I believe that the current industry trend of deep learning is useful but ultimately a dead-end in the pursuit of general artificial intelligence. Current intelligence, as exhibited by lifeforms, has come about through the process of life. Intelligence has evolved as a competitive advantage for life. I’ve heard it stated that it is a hard question to ask “what is (general AI) intelligence?”. To me the answer is simple: Intelligence is the computational aspects of life that aid life. I think the path to finding how to create general AI will be through understanding life. Further, I think that general AI will not be possible without, in some sense to be found, it being exhibited by life. If that is true, it has deep implications for our future relationship with these lifeforms.